Почему велосипед не падает

Почему велосипед не падает, не вполне понятно, особенно на первый взгляд. Площадь его опоры очень мала, даже если шины весьма широкие и слабо накачаны. Поставленный вертикально, он долго не простоит. Обычно он падает на бок через 2 - 4 секунды, но если его удачно толкнуть вперед, падение случится через 10 - 15 секунд. Именно этим велосипед решительно отличается от трёхколесного велосипеда и четырехколесного автомобиля. Даже если отбросить влияние велосипедиста на устойчивость, то во время езды велосипед гораздо устойчивей, чем во время остановки. Управляться он может также по-разному, и не только поворотом руля. Если вспомнить езду «без рук», то становится понятно, что факторов, обеспечивающих устойчивость велосипеда, несколько. Рассмотрим главные. Но прежде, еще одно короткое замечание: у велосипеда существуют две устойчивости и одна управляемость. Первая устойчивость — это вертикальная, вторая — продольная, или курсовая устойчивость, а управляемость — только продольная (курсовая). Само собой, чем лучше продольная устойчивость, тем хуже управляемость, и наоборот. Сложность заключается во взаимосвязи этих трех важных параметров. Один влияет на другой, другой на третий и рассказать, положим, о вертикальной устойчивости, не упоминая продольную, затруднительно. Но в любом случае, каждому практикующему велосипедисту важно сохранить равновесие, или баланс и катить в правильном направлении.

Равновесию на малой скорости или даже стоя на месте, как лихо демонстрируют некоторые умельцы, помогает геометрия вилки и рулевой колонки. Поворачивая руль, мы сдвигаем центральную линию велосипеда, проходящую через точки контакта с поверхностью переднего и заднего колес. Так мы подстраиваем ее под слегка сдвинувшийся в сторону центр тяжести велосипедиста и его верного двухколесного коня. Балансирование на месте всем хорошо известно и знакомо — это сюрпляс. Подробно о полезных свойствах вилок и их влиянии на устойчивость можно посмотреть чуть ниже.

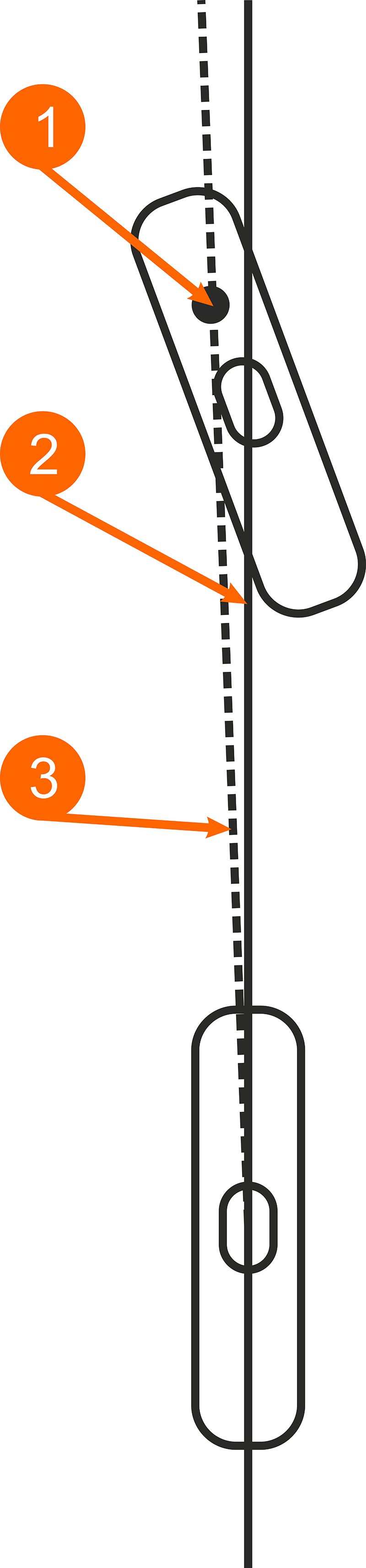
Вид сверху показывает, как эту линию шин можно сдвинуть в сторону поворачиванием руля из стороны в сторону. Это очень важно для баланса на низкой скорости.

1. Ось поворота на уровне земли
2. Линия через пятна контакта шин
3. Центральная линия

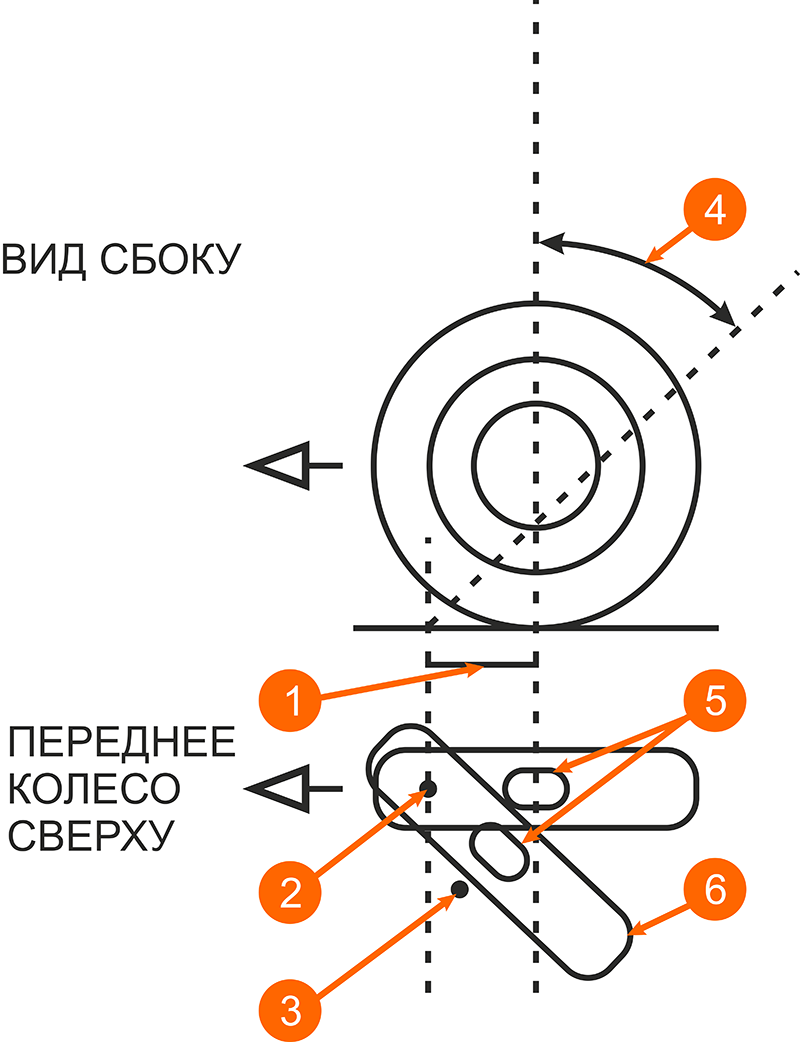
1. Вылет
2. Ось рулевой колонки на уровне земли
3. Боковая сила из-за угла скольжения
4. Наклон
5. Пятно контакта шины с дорогой
6. Отклонённое колесо

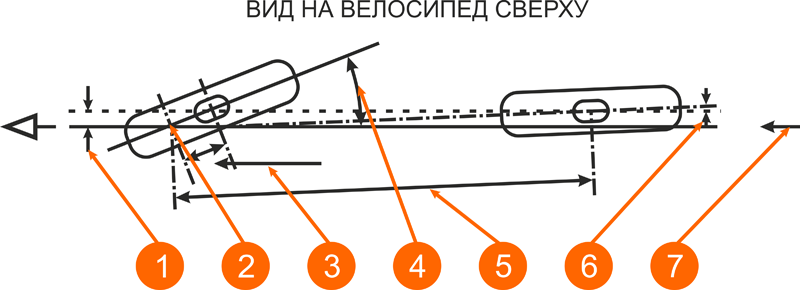
1. 1/2 дюйма
2. Ось рулевой колонки на уровне земли
3. Передний вылет
4. 7 - 10 грудусов
5. Задний вылет
6. 1/2 градуса
7. Линия движения

Какую скорость считать малой, а какую — большой? Это нетривиальный вопрос. Но все-таки можно получить приблизительную оценку минимальной скорости устойчивого движения велосипеда. Помогает этому теория движения твердого диска (обруча, колеса) по плоскости без проскальзывания. Согласно ней, для обеспечения устойчивости такого диска, близкого к диаметру велосипедного колеса, достаточно скорости около 1 м/сек, или 3,6 км/час.

Скорость ниже минимальной — это уже искусство балансирования, или сюрпляс на треке. Система, составленная из велосипеда и велосипедиста, конечно, очень далека от простого катящегося диска или обруча, но данное значение показывает порядок величины минимальной скорости, необходимой, чтобы устойчиво держаться на велосипеде. И, как каждому хорошо известно, имеет приближенное согласие с повседневным опытом.

Но ведь велосипед — это вам не какой-нибудь «Харлей». Велосипедист весит гораздо больше, чем велосипед, на котором он сидит. Поэтому чтобы держать равновесие на велосипеде в некоторых ситуациях, например, на узкой колее, тропинке, лыжне можно перемещать центр тяжести как вправо, так и влево, меняя положение тела велосипедиста относительно велосипеда. Нужно, как бы отталкиваясь от него в сторону, противоположную первоначальному отклонению, сохранять равновесие, продолжая неуклонное движение вперед. При этом более высокий центр тяжести велосипедиста сильнее воздействует на общий баланс системы велосипедист - велосипед и дает больший контроль над положением и движением велосипеда. Еще один полезный способ движения корпусом при рулении рассмотрим ниже.

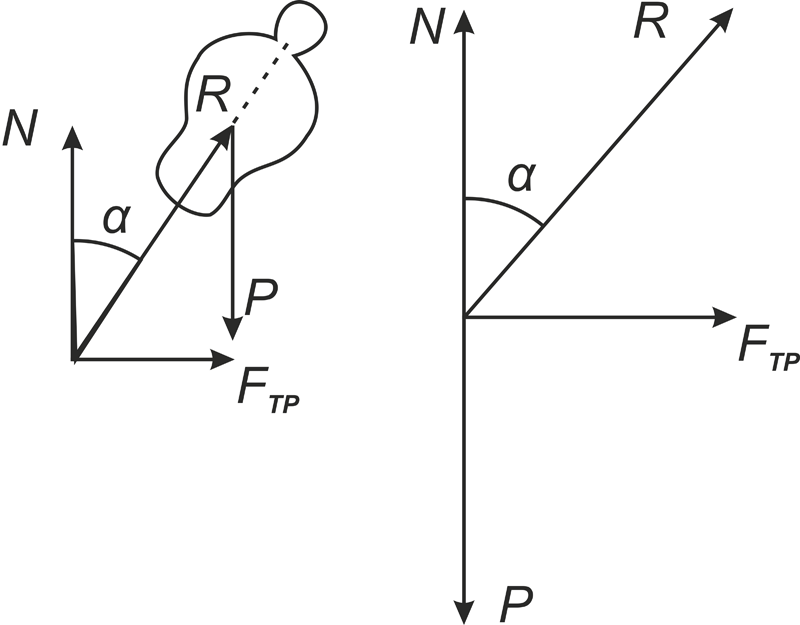
Представим себе обычный случай: велосипедист поворачивает со скоростью v по кругу с радиусом R. Для сохранения равновесия велосипедист должен наклониться на угол α от вертикали или, что тоже самое, на угол φ=90° - α от горизонтали, чтобы компенсировать центробежную силу (смотрите рисунок выше). Условия равенства сил приводят к известной еще со школы элементарной формуле ctg α=(v²/gR)=tgφ≤μ (1), где μ — максимально возможный в данный момент коэффициент сцепления шины с дорогой. Для реальной оценки его надо уменьшать на 20 - 25% по сравнению с многочисленными табличными значениями, g — ускорение свободного падения, равное 9,81 м/сек. Велосипедист поворачивает благодаря силам трения между дорогой и передним колесом. Если дорога скользкая или покрыта льдом, то контролируемый поворот становится затруднительным или невозможным. Вместо поворота может произойти занос переднего колеса, потеря равновесия и падение.

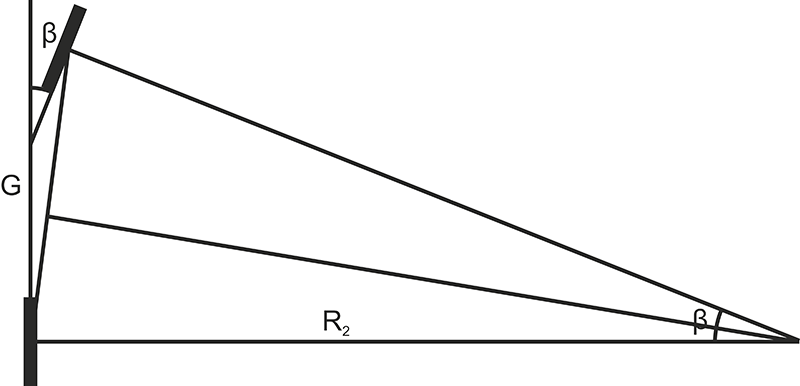
Пусть теперь велосипедист, спокойно катясь по прямой, ровной и гладкой дороге и любуясь проплывающим мимо пейзажем, случайно отклонился от вертикали на небольшой угол α_l. Чтобы не упасть, велосипедист старается повернуть руль в сторону наклона велосипеда на угол β. Спрашивается, на какой угол надо повернуть руль, дабы не упасть? Для ответа достаточно посмотреть на рисунок выше и вспомнить любимую теорему синусов G=2R₂sinβ (2), где G — расстояние между осями колес (база велосипеда), R₂ — радиус, по которому начинает двигаться велосипед после поворота переднего колеса. Он должен быть меньше, чем радиус, по которому спокойно и уверенно поворачивает велосипедист, отклонившись от вертикали на угол α_l, согласно формуле (1). Иначе выправить равновесие не удастся. Теперь подставим формулу (2) в формулу (1). И получим: sin β=(gGtgαl/2v²) (3). Эта очень простая формула может рассказать много полезного.

Первое. Велосипедисту, катящемуся со скоростью v и отклонившемуся от вертикали на угол α_l, нужно повернуть руль на угол больший или равный углу β, который легко подсчитать по формуле (3).

Второе. Чем больше скорость велосипедиста, тем на меньший угол надо повернуть руль и для восстановления равновесия и для прохождения виража. Из этого следует, что велосипедом намного легче управлять на высокой скорости, чем на маленькой. И это хорошо известно всем, кто садился на велосипед.

Третье. Чем больше база велосипеда — G, тем на больший угол надо поворачивать руль, дабы восстановить равновесие или вписаться в поворот. И так же интуитивно ясно, что по узким, лесным извилистым дорожкам легче катить на велосипеде с малой базой.

Четвертое. Навык правильного поворота руля быстро становится автоматическим, подсознательным, и многие велосипедисты не подозревают, что даже при беззаботной езде по прямой им нужно постоянно поворачивать руль. Достаточно посмотреть на след, оставленный колесами велосипеда. Легко увидеть, что относительно прямая колея, оставленная задним колесом, всё время пересекается извилистым следом переднего. А это значит, что переднее колесо во время движения постоянно поворачивает из стороны в сторону, велосипед все время «въезжает» под регулярно падающего велосипедиста и, благодаря этому, сохраняет равновесие.

И, наконец, пятое. Если руль не поворачивается, если рулевая колонка, положим, по каким-то причинам заклинена, ездить практически нельзя (в современном понимании этого слова). Двухколесные самокаты начала XIX века, не имевшие рулевого управления, могли катить только по прямой.

И это приводит нас к любопытной аналогии между сохранением равновесия на велосипеде и удержанием швабры, бильярдного кия или авторучки («Паркер» с золотым пером, например) на раскрытой ладони. Действительно, как удержать кий? Сначала он стоит на ладони вертикально, а затем начинает отклоняться, и ладонь быстро перемещается в сторону наклона. Опора кия смещается, и он начинает наклоняться в другую сторону. Ладонь снова перемещается, и такое балансирование может длиться весьма долго.

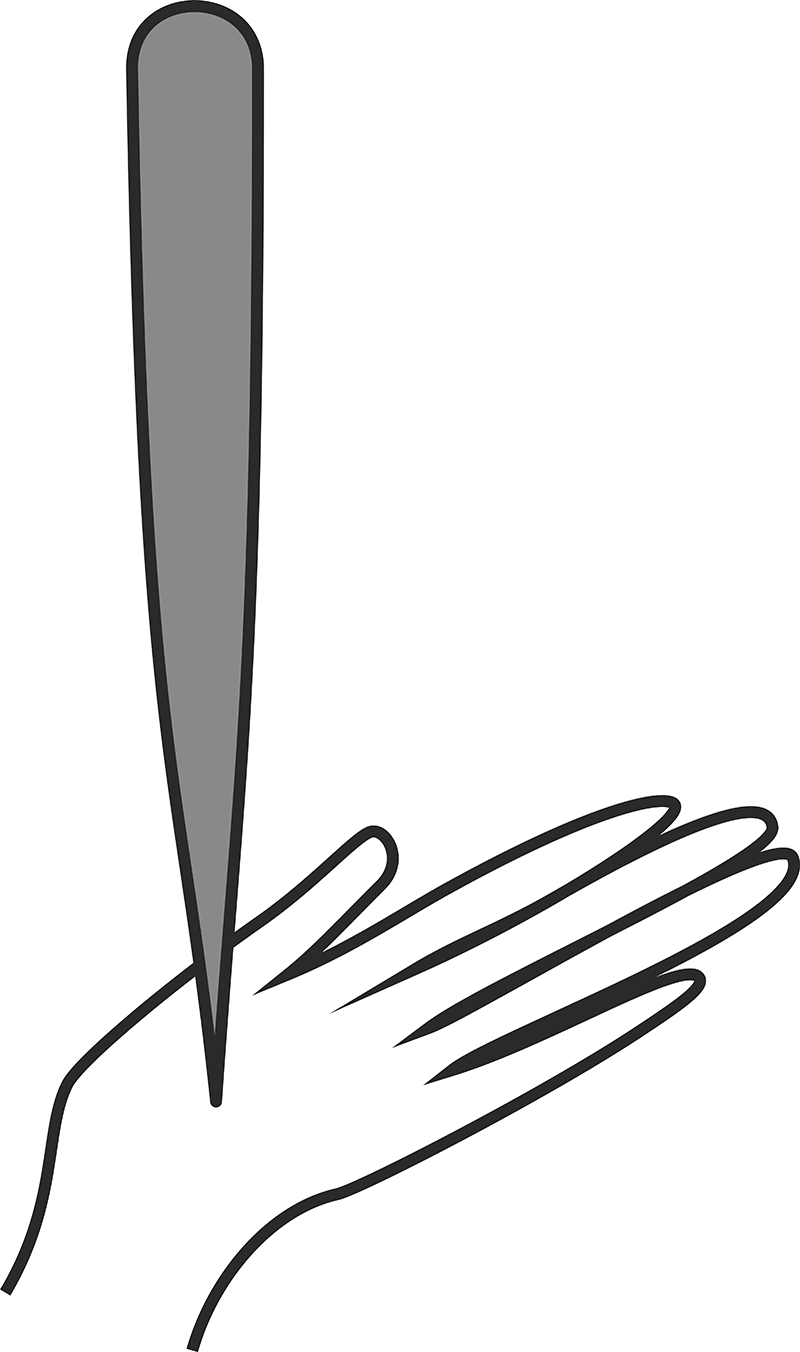
То же самое делает и велосипедист. Но возникает естественный вопрос: чем проще балансировать — шваброй или авторучкой? Ответ не вполне очевиден, но, твердо освоив школьный курс на «хорошо», получить правильный результат несложно. Прежде всего, на что похожи стоящая швабра, авторучка и катящийся велосипед? Правильно! На перевернутый физический маятник. Вместо точки подвеса есть точка опоры. И такие перевернутые маятники всем хорошо знакомы — например, механический метроном, которым задают ритм при изучении музыки. Чем выше поднимают грузик на планке, тем больше период колебаний, и тем медленнее качается маятник метронома. А если грузик опустить вниз, к точке опоры, то период колебаний уменьшится, и маятник быстро-быстро зачастит.

С некоторыми оговорками и при малых отклонениях от вертикали его можно рассмотреть как математический маятник и написать крайне простую формулу для периода колебаний. T≈2π√l/g, где l — расстояние от точки опоры до центра масс (ЦМ). Время отклонения от вертикали на малый угол α1 равно: t=T/4≈(π/2)√l/g. Оно не зависит от массы швабры и «откормленности» велосипедиста. Прикинем: швабра имеет l=1м, 1=1,6*0,32=0,5 с. У авторучки же l=0,1 м, t= 1,6*0,1=0,16 с. А высокий велосипед — l=1,2 метра, t= 1,6*0,35=0,56 с. Результат прост и нагляден.

Точно так ведет себя и любой предмет: чем он выше, чем больше расстояние от точки опоры до центра масс (центра тяжести), тем медленнее он отклоняется от вертикали на малый угол, и тем легче им балансировать или удерживать на нем равновесие. И тут вне конкуренции велосипед «Паук», у которого центр масс располагался на высоте около двух метров. Но падать с такой высоты было больно и опасно, и «Пауки» не выжили. Поэтому намозолившее глаза выражение «низкий устойчивый силуэт» справедливо только для трех или четырех колесных экипажей. Если так говорят о двухколесных велосипедах или мотоциклах, то это нонсенс и техническая безграмотность.